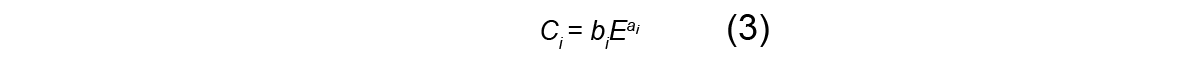Optimal Targeting of a Tumor through Proton Beam Therapy

Kiran Pant and Colin Campbell

Washington College 300 Washington Ave. Chestertown, MD 21620

Duke University Graduate School 2127 Campus Dr. Durham, NC 27705

University of Mount Union 1972 Clark Ave. Alliance, OH 44601 

ABSTRACT

Proton beam therapy is an effective treatment option for deep-seated tumors. Although the behavior of protons as they travel through tissue is well understood, there are significant technological challenges involved in generating and optimizing a beam to effectively treat a specific tumor. Proton therapy Monte Carlo simulation packages require designated operating systems and software, thus making it difficult to study the effects of a proton beam in a non-clinical setting. Here we seek to (1) develop a model that captures the salient physics while simulating a proton beam entering the body given the beam energy and beam width, and (2) optimize these properties to effectively target a simulated tumor in three dimensions. All simulations are created in Python. First, three separate one-dimensional Bragg curves at energies 150 MeV, 200 MeV, and 250 MeV are simulated to demonstrate the energy deposition of protons as they traverse matter. A two-dimensional monoenergetic proton beam is then simulated in the context of targeting a circular tumor by approximating the range by the Bragg-Kleeman rule, and then a complete three-dimensional case is studied similarly, in the context of targeting a spherical tumor. The optimization performed in this study determines the beam width and energy that maximizes the amount of energy deposited in the tumor and minimizes energy deposition to surrounding tissue. The results indicate that a constricted beam can constrain the energy deposition maximally to the tumor, and we identify the optimal energy to effectively target the simulated tumor. Specifically, we show that in our modeling framework a spherical tumor with a 2 cm radius with its center located 6 cm inside the body is most effectively targeted with a 99 MeV beam. This work demonstrates the ability to simulate a proton beam in two- and three-dimensions at therapeutic energies. 

INTRODUCTION

In 1946, physicist Robert Wilson proposed the idea to treat deep-seated tumors in the body using accelerated proton beams (Wilson, 1946). The concept and theoretical framework of proton beam therapy (PBT) has expanded significantly, and the Particle Therapy Cooperative Group (PTCOG) reported that over 180,000 patients have been treated with PBT as of 2018. Patients with tumors that have well-defined margins and are in situ benefit the most from this treatment method due to the ease of targeting a well-delineated and immobile tumor. This can include patients with cancers of the prostate, esophagus, lung and liver. A large number of pediatric patients with central nervous system (CNS) tumors also benefit from PBT (Gondi et al., 2016).

Protons interact with matter in three different ways: interactions with atomic electrons, interactions with the atomic nucleus, and interactions with the atom as a whole (Verhey et al., 1998). Protons that interact with the nucleus may produce Bremsstrahlung radiation, but this occurs so infrequently that its effects are negligible. There is also the possibility that protons will collide with an atom and produce secondary protons, neutrons, or excited nuclei, although these interactions are also rare. Protons primarily lose kinetic energy as they traverse matter via inelastic Coulombic interactions with atomic orbital electrons, which also deflect the proton trajectory (Newhauser and Zhang, 2015). The deflection due to a single interaction is generally quite small as the mass of a proton is much larger than that of an electron. However, the cumulative effect of many such interactions can be significant. The most complete theory of multiple Coulombic scattering was proposed by Molière (1947). Many simplifications of this theory have been proposed, although this simplicity often reduces the accuracy in modeling Coulombic scattering at large angles. Gottschalk et al. (1993) approximated Molière’s theory to take the form of a Gaussian function, assuming the small angle approximation in which sin(θ)≈θ:

where [(θ²)^1/2] is the root mean square (rms) scattering angle of the Gaussian distribution. Abril et al. (2015) showed that the rms width of the distribution varies parabolically with depth z :

where distances are measured in micrometers and the parameters C₁ and C₂ depend on the initial energy of the beam according to:

Here, the beam energy E is measured in MeV and the parameters a_i and b_i are material-dependent constants. In this report, we use these equations to characterize how the width of the beam grows with depth, starting from an initial angular width s₀ .

The linear stopping power, or energy loss rate, of protons as they travel through matter is the average energy loss per unit distance. Bloch (1933) developed a detailed treatment of this phenomena that takes into account relativistic effects. Bloch demonstrated that accelerated protons’ energy loss rate is proportional to the inverse square of its velocity. Thus, as protons slow down, their interaction cross section increases and more energy is deposited toward the end of their track. Once they come to rest there is no more energy deposition. This characteristic of protons is referred to as the Bragg curve. This can be described by a simple mathematical formula based on the Bragg-Kleeman rule (Bragg and Kleeman, 1905), which was originally developed for alpha particles:

Here S/ρ is the mass stopping power, E is the particle’s energy, ρ is the density of the material, p is a constant that considers the particle’s velocity, and α is a material-dependent constant.

The range of a proton beam is defined as the depth at which half of the protons in the medium come to rest. Proton particles in a beam do not come to rest at the same time; there are small variations in the energy loss rate of each individual particle, causing them to come to rest at various distances (Newhauser and Zhang, 2015). This effect is referred to as range straggling, and although it helps to shape the proton Bragg curve, it does not play a critical role for dosimetry purposes in the clinic. A first order approximation for the range is calculated using the Bragg-Kleeman rule:

As before, α is a material-dependent constant, E is the particle’s energy, and the exponent p is a constant that considers the particle’s velocity.

Protons are directly ionizing radiation, meaning that they interact with cellular atoms or molecules and produce free radicals. Free radicals, such as hydroxyl, can be hazardous to all major components of the cell. They contain unpaired electrons and seek out surrounding atoms to strip an electron from their orbit, which ultimately damages the cell. Free radicals induce single and/or double strand breaks on DNA, which can either kill or mutate the cell if the cell is unable to repair itself (Girdhani et al., 2013). Therefore, it is imperative to spare healthy tissue during radiation therapy; killing or mutating healthy tissue may lead to more acute radiation effects and may induce secondary cancer in the patient. Due to the nature of the trajectory of protons, PBT is most beneficial for patients with tumors that are localized and are situated near organs at risk (Merchant et al., 2008). This offers a strong advantage over photon beam therapy in which maximum energy deposition is located closer to the surface of the skin, and then gradually decreases over some range (Levin et al., 2005). As protons deposit their maximal energy near the end of their path with a finite range, this ensures tissues anterior and posterior to the tumor receive a minimal dose.

Recent research shows that there are advantages in using PBT compared to photon beam therapy in terms of focusing energy deposition in the target so as to spare normal tissue (Brada et al., 2009; Paganetti et al., 2002). However, the roles of tumor type and location have not been fully explored. The Monte Carlo simulation is a useful computational tool that probabilistically samples proton trajectories to predict the average behavior (i.e. energy deposition pattern) of a proton beam. The average beam is determined by repeatedly sampling proton trajectories; each trial uses a different set of values. Clinical implementation of Monte Carlo dose calculations for proton beam therapy are currently being developed and tested (Perl et al., & Paganetti, 2012). They are found to be more accurate than analytical algorithms because of the more detailed consideration of tissue interaction. 

Although Monte Carlo calculations present clinical advantages in optimizing proton treatment planning and accounting for tissue interaction, more research is needed to fully understand why protons interact with tissue in the way they do. In addition, the software packages that perform Monte Carlo calculations are difficult to access outside of a clinical setting. Rather than focusing on these clinical details, the purpose of this study is to apply analytical algorithms to simulate a proton beam in one-, two- and three-dimensions to capture the core physics in a straightforward and accessible modeling framework. The energy deposited within a modeled tumor is calculated, and the parameters that minimize the energy deposited outside the tumor while maximizing the amount of energy deposited in the tumor are determined. As a case study, the optimal parameters for a circular and spherical tumor are determined.

METHODS

One-Dimensional Bragg Curve Simulation

Three separate Bragg curves are simulated using Python (version 3.6.9) at energies 150 MeV, 200 MeV, and 250 MeV. We used Equation 4 to construct these curves and use the parameters for water as this is a reliable tissue-equivalent: α = 2.633 E-3, ρ = 1 g/cm³, and ρ = 1.735 (Newhauser and Zhang, 2015)

Target Parameters in Two and Three Dimensions

We assume that the proton is aligned with the midpoint of the tumor, which is a circle in two-dimensions or a sphere in three dimensions with radius r. We denote the distance from the surface to the midpoint of the tumor d. To be specific, we consider r = 2 cm and d = 6 cm. 

Simulated Proton Beam in Two Dimensions

A computer program developed in Python determines the energy loss rate of a two-dimensional proton beam and simulates how the beam spreads through a circular tumor and surrounding tissue using Equations (1 - 4). When describing the rms width of the energy distribution curve with Equations (2 - 3), we use the parameter values for water: a₁ = -0.058 ± 0.008, a₂ = -1.868 ± 0.010, b₁ = (9.39 ± 0.14) × 10^-3, b₂ = (1.56 ± 0.03) × 10^-3 (Abril et al., 2015) and we similarly use the water-equivalent parameters for Equation (4) described above. The numerical integral of the energy deposition is calculated (in MeV) to confirm energy conservation; we also specifically calculate the energy deposited over the tumor to evaluate the efficacy of the beam.

The simulated proton beam and energy dispersion in two and three dimensions are created using a range of energies from 85 MeV to 105 MeV with a step size of 2 MeV. For each value of energy, the initial beam width is systematically varied from 0.1 rad to 0.3 rad with step size 0.05 rad, for a total of 55 simulations.

The optimal beam energy, E₀ , and beam width, s₀ , are determined by evaluating the difference between the energy deposited in the tumor and the energy deposited in the surrounding tissue:

An objective function created in Python determines the initial energy and beam width that maximize this difference:

These optimal values are then used to create a top-down and perspective view of an optimized proton beam. 

Simulated Proton Beam in Two Dimensions

Figure 1. Simulated Bragg curves (energy loss rate as a function of depth) of 150 MeV, 200 MeV, and 250 MeV protons shown in blue, green, and red, respectively. Figure (a) shows the Bragg curves on a log scale axis, and Figure (b) shows the Bragg curves on a standard axis.

While the task of projecting a three-dimensional beam onto a two-dimensional plane can be complex (Newhauser and Zhang, 2015), we here model the generalization of the two-dimensional beam to three-dimensions by first noting that the angular component (in cylindrical coordinates) of the energy dispersion is uniform in three dimensions. For example, there is no tendency for the beam to deflect up instead of down from the initial orientation of the beam. 

Figure 2. Objective function for a range of proton beam energies and widths in terms of the standard deviation of a Gaussian, s. The initial beam energy ranges from 80 MeV to 100 MeV with a step size of 2 MeV. The target tumor has a radius, r, of 2 cm with a distance from the surface to the midpoint of the tumor, d, of 6 cm.

Thus, we consider the energy that is deposited to a unit area inside a circular (two-dimensional) tumor to, in the case of a (three-dimensional) spherical tumor, be evenly deposited in a unit volume in the form of a ring in the three-dimensional case. In this framework the total energy deposited within the tumor is identical in both the two-dimensional and three-dimensional scenarios.

Accuracy of Simulation

To access the accuracy of the simulations used in this report, the depth values at maximum dose deposited are compared to the values established by the National Institute of Standards and Technology (Berger et al., 2017). This analysis is performed for the one-dimensional Bragg curves and two- and three-dimensional proton beams simulated at 150 MeV, 200 MeV, and 250 MeV.

Source Code

All code used in this report is available at https://github.com/ColinECampbell/proton_beam.

RESULTS

Bragg Peak Simulation

Three one-dimensional Bragg curves at 150 MeV, 200 MeV, and 250 MeV traveling through water are shown in Figure 1. The peaks occur at depths of 15.70 cm, 25.87 cm, and 38.10 cm, respectively, demonstrating the nonlinear relationship between the Bragg peak and the initial energy (Equation 4). We note also that, perhaps counterintuitively, increasing the beam energy leads to a decrease in the magnitude of the Bragg peak. This is due to the energy loss in the broader region between the surface of the material and the Bragg peak; as we show below, this behavior is important when considering coverage of a target with appreciable size, such as a tumor.

Two- and Three-Dimensional Simulated Proton Beam

All two-dimensional simulations were completed in approximately 10 minutes on a modern computer. Figure 2 shows the objective function for varying beam energies and beam widths; as the figure shows, the optimal parameters are s₀ = 0.1 rad and E₀ = 99 MeV.We additionally show the fraction of the beam energy provided to the tumor in Table 1; the same optimal parameters are identified. Figure 3 uses these parameters to show the target (as a black surface) along with the energy deposition of the proton beam. Because a two-dimensional beam is being considered, we show the energy deposition as the vertical coordinate. The main source of error in these simulations is due to the sharpness of the Bragg peak, which can complicate the numerical integration of the energy deposition. However, the difference between the calculated beam energy and the initial beam energy was on average only 2.7%.

The initial energy of the beam, which controls the depth of the Bragg peak (Figure 1), is optimized to place the Bragg peak near the rear of the tumor. This maximizes the amount of the pre-peak energy deposition delivered to the tumor. Figure 1 also demonstrates the effect of the beam spread, which is significant relative to the target even for the narrowest beam considered. As the figure shows, in this case the spread serves to provide nontrivial coverage to most of the tumor. For example, approximately 73% of the tumor area receives a mass stopping power of at least 10 MeV cm^-1. Figure 4 shows the same beam in three dimensions. Because each axis necessarily corresponds to a spatial coordinate, we show energy deposition with a colorized surface: at any position, the surface encloses 80% of the energy deposited at the corresponding depth.

For both two- and three-dimensional simulated proton beams, the peaks occur at 15.70 cm, 25.90 cm, and 38.1 cm at 150 MeV, 200 MeV, and 250 MeV respectively.

Accuracy of Simulation

The theoretical peak depth values occur at 15.76 cm, 25.93 cm, and 37.90 cm for a 150 MeV, 200 MeV, and 250 MeV, respectively (Berger et al., 2017). This corresponds to a percent error of less than 1% for all values produced in this study.

DISCUSSION

Figure 3. (a) Top-down view and (b) perspective view of a simulated proton beam optimally entering the system. In these figures, yellow represents maximal energy deposition. A circular tumor is simulated and is shown as a dark, shaded region on the plots above.

Figure 4. Energy dispersion of a proton beam in three dimensions. The target is here shown as a gray wireframe; the colorized surface contains 80% of the energy deposited at a given depth (x coordinate), with the total energy at that depth represented by surface color.

The results demonstrated in this study are consistent with those demonstrated in clinical practice of PBT. The Bragg curves shown in Figure 1 demonstrate that higher energy beams deposit their energy at a greater depth within the body, which is consistent with the fact that higher energy beams are used to treat deep-seated tumors. The Bragg curves are also able to demonstrate the useful property of protons having a finite range and a focused depth at which a significant portion of their energy is deposited: after the Bragg peak has been reached, protons deposit negligible energy within a medium. This ensures that healthy tissue situated posterior to the tumor is unaffected during treatment.  

It is important to note that more detailed models are used for treatment planning than the model presented in this study. More complete models account for tissue-specific interactions and consider the radiobiological effects of treating a patient with proton therapy. For example, the calculations performed in this study employed the common simplification of treating tissue as uniformly equivalent to water (Newhauser and Zhang, 2015) for the sake of determining general parameters that affect a simulated tumor. While this approach is beneficial for studying the main principles that characterize the dispersion of energy due to a proton beam and successfully demonstrates the relationship between the initial beam energy and the depth of the Bragg peak (i.e. the depth of the tumor for an optimized beam), the omission of the above-mentioned considerations clearly makes this model inappropriate for clinical implementation. 

While we have successfully simulated two- and three-dimensional proton beams entering water (a commonly used tissue equivalent framework), we have assumed a monoenergetic proton beam for treatment. This means that only a narrow depth range can be treated with the Bragg peak. To accommodate the entire tumor, a spread-out Bragg peak (SOBP) is often created to widen the Bragg peak and increase the area of dose distribution to the tumor. This is accomplished by varying the energy of the incident proton beam and using various energies to produce a flat SOBP. Simulation studies of SOBP typically employ time-consuming Monte Carlo methods (Jette and Chen, 2011). 

These results demonstrate important characteristics of proton beams that make this method of treatment more beneficial for well defined, deep seated tumors compared to photon therapy. Protons primarily deposit dose at a localized depth corresponding to the energy of the incident beam, whereas photons deposit dose maximally near the surface; the dose decays as it penetrates the body. Overall, the missing exit dose and the confined energy deposition characteristics with protons are superior to those of photons for patients with deep-seated tumors. 

There are several possible extensions for future research. We have approached our simulations using simplified models to capture the dominant behavior of the proton beam deposition; a more complete and accurate simulation of the proton beam would require more rigorous calculations using Bohr’s formula for the linear stopping power and Molière’s theory on multiple Coulombic scattering. We have also assumed the shape of a tumor to be perfectly symmetrical, whereas, in reality, tumors can be different shapes and sizes. Future extensions of this work can include changing the tumor’s physical properties and/or its location within the body. In addition, more even coverage over a tumor could be achieved by incorporating a range of initial beam energies to generate a spread-out Bragg peak and/or allowing for a moving beam source. 

REFERENCES

1. Abril, I., de Vera, P., Garcia-Molina, R., Kyriakou, I., and Emfietzoglou, D. (2015). Lateral spread of dose distribution by therapeutic proton beams in liquid water. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 352, 176–180. available: https://doi.org/10.1016/j.nimb.2014.11.100.

2. Berger, M. J., Coursey, J. S., Zucker, M. A., and Chang, J. (2017). Stopping-power and range tables for electrons, protons, and helium ions. available: https://www.nist.gov/pml/stopping-power-range-tables-electrons-protons-and-helium-ions.

3. Bloch, F. (1933). Zur Bremsung rasch bewegter Teilchen beim Durchgang durch Materie. Annalen Der Physik, 408(3), 285–320. available: https://doi.org/10.1002/andp.19334080303.

4. Brada, M., Pijls-Johannesma, M., and De Ruysscher, D. (2009). Current clinical evidence for proton therapy. The Cancer Journal, 15(4), 319–324. available: https://doi.org/10.1097/PPO.0b013e3181b6127c.

5. Bragg, W. H., and Kleeman, R. (1905). The alpha particles of radium, and their loss of range in passing through various atoms and molecules. London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 10(57), 318. available: https://search.proquest.com/docview/1309447316?accountid=10598&pq-origsite=summon.

6. Girdhani, S., Sachs, R., and Hlatky, L. (2013). Biological effects of proton radiation: what we know and don’t know. Radiation Research, 179(3), 257–272. available: https://doi.org/10.1667/RR2839.1.

7. Gondi, V., Yock, T. I., and Mehta, M. P. (2016). Proton therapy for paediatric CNS tumours — improving treatment-related outcomes. Nature Reviews Neurology, 12(6), 334–345. available: https://doi.org/10.1038/nrneurol.2016.70.

8. Gottschalk, B., Koehler, A. M., Schneider, R. J., Sisterson, J. M., and Wagner, M. S. (1993). Multiple Coulomb scattering of 160 MeV protons. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 74(4), 467–490. available: https://doi.org/10.1016/0168-583X(93)95944-Z.

9. Jette, D., and Chen, W. (2011). Creating a spread-out Bragg peak in proton beams. Physics in Medicine and Biology, 56(11), N131–N138. available: https://doi.org/10.1088/0031-9155/56/11/N01.

10. Levin, W. P., Kooy, H., Loeffler, J. S., & DeLaney, T. F. (2005). Proton beam therapy. British Journal of Cancer, 93(8), 849–854. available: https://doi.org/10.1038/sj.bjc.6602754.

11. Merchant, T. E., Hua, C., Shukla, H., Ying, X., Nill, S., & Oelfke, U. (2008). Proton versus photon radiotherapy for common pediatric brain tumors: Comparison of models of dose characteristics and their relationship to cognitive function. Pediatric Blood & Cancer, 51(1), 110–117. available: https://doi.org/10.1002/pbc.21530.

12. Moliere, G. (1947). Theorie der Streuung schneller geladener Teilchen I. Einzelstreuung am abgeschirmten Coulomb-Feld. Zeitschrift Für Naturforschung A, 2(3), 133–145. available: https://doi.org/10.1515/zna-1947-0302.

13. Newhauser, W., and Zhang, R. (2015). The physics of proton therapy. Physics in Medicine & Biology, 60(8). available: https://doi.org/10.1088/0031-9155/60/8/R155.

14. Paganetti, H., Niemierko, A., Ancukiewicz, M., Gerweck, L. E., Goitein, M., Loeffler, J. S., & Suit, H. D. (2002). Relative biological effectiveness (RBE) values for proton beam therapy. International Journal of Radiation Oncology, Biology, Physics, 53(2), 407–421. available: https://doi.org/10.1016/S0360-3016(02)02754-2.

15. Perl, J., Shin, J., Schümann, J., Faddegon, B., and Paganetti, H. (2012). TOPAS: An innovative proton Monte Carlo platform for research and clinical applications. Medical Physics, 39(11), 6818–6837.available: https://doi.org/10.1118/1.4758060.

16. Verhey, L., Blattman, H., Deluca, P. M., and Miller, D. (1998). 4. Proton Interactions with Matter. Journal of the International Commission on Radiation Units and Measurements, os30(2), 13–14. available: https://doi.org/10.1093/jicru/os30.2.13.

17. Wilson, R. R. (1946). Radiological Use of Fast Protons. Radiology, 47(5), 487–491. available: https://doi.org/10.1148/47.5.487.