Author: Matthew Benesh
Institution: Baylor University
Date: January 2007
Abstract
The box_tree code is used to simulate the formation of 12-particle three-dimensional Yukawa dust clusters within a complex plasma. The structure of the cluster is analyzed; in particular, the potential energy is calculated for all clusters that fall into stable single-shell states and also for all clusters that fall into stable double-shell states. It is shown that the ground state may be either single-shell or double-shell, depending on the given Debye length. The dependence of cluster structure on Debye length is analyzed quantitatively.
I. INTRODUCTION
A complex (dusty) plasma is a mixture of electrons, ions, and small dust particles with radii on the order of a few microns. As the dust particles move through the plasma, they collect a net negative charge, due to the increased mobility of electrons as compared to the positive ions ([Chu et al. 1994)]. As the negative charge increases in magnitude, positive ions in the plasma are attracted to the dust particles, inducing a shielding effect. This shielding effect produces a Yukawa system, with a Yukawa potential
article_883_order_2
, (1)
describing the electric potential around each dust particle [Qiao & Hyde 2005](Qiao & Hyde 2005). In Equation (1), q is the net charge on the dust particle, r is the distance between any two particles, and λD is a quantity known as the Debye length. The dust Debye length is the distance at which the positive ions effectively shield the negative charge on the dust particle.
When a complex plasma is confined within a potential well, as in laboratory experiments ([Rafac et al. 1991)], the individual dust particles are forced to interact. In microgravity conditions, or in the presence of a force opposed to gravity, such as a thermophoretic force, the particles will form what are known as Coulomb clusters', and in the case of a Yukawa system, Yukawa clusters'. Each of these clusters is an arrangement of particles in spherical shells, exhibiting specific structure. This phenomenon has been thoroughly investigated; for example, Arp et al. (2005) conducted experimental and theoretical experiments tests to determine the shell configuration for varying numbers of dust particles, as well as the fine structure' of those configurations.
The shell configuration mentioned above refers to the number of dust particles present in each shell. For example, it has been shown that a cluster of ten dust particles may be comprised of a single shell occupied by ten particles, or two shells, with the outer containing nine particles and a single particle occupying the center of the cluster (Arp et al. 2005). As the total number of dust particles increases, the shells will continue to fill until it becomes more energetically stable to form a new shell, at which point particles move toward the center of the cluster and generate a new structure. For example, Arp et al. (2005) have shown that a 160-particle cluster in its most stable configuration occupies four shells, with the outermost containing 102 particles, and the innermost consisting of a single particle.
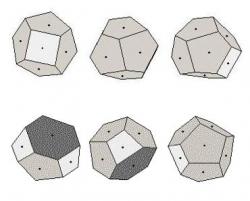
Figure I. Voronoi construction for the cluster N = 10. The upper row shows three orientations of the ground state; the lower row shows three orientations of a metastable (excited) state. White cells are quadrilaterals, gray cells are pentagons, and dark cells are hexagons.
The term fine structure' refers to the arrangement of particles within each shell. This structure is most often investigated through the use of Voronoi diagrams. A Voronoi diagram is composed of cells that each contains a single particle. The borders of each cell are created by bisecting the axis between the central particle and each of its nearest neighbors. Voronoi diagrams as applied to dust crystals are useful in determining interactions between any one particle and its closest neighbors, which is the prime determinant of the amount of potential energy within the cluster's fine structure. A slight change in the fine structure of a crystal from its ground state will slightly increase its potential energy, creating what is known as a metastable state. Examples of a stable cluster and a metastable cluster divided into Voronoi cells are shown in Fig. I. A thorough survey of Voronoi analysis is given in Aurenhammer (1991).
II. METHODS
The box_tree code [Qiao & Hyde 2005](Qiao & Hyde 2005) was used to model theoretical complex plasmas, yielding Yukawa clusters. The code simulates a given number of charged dust particles confined by a parabolic external potential, as defined by
article_883_order_3
(2)
where x, y, z define the particle location and k is the magnitude of the confinement [Qiao & Hyde 2005](Qiao & Hyde 2005). Utilizing a random number seed, the code places the dust particles at randomized locations within this potential "box", and assigns them random velocities. Kinetic energy is lost through friction caused by gas drag. The simulation is allowed to run until the system reaches thermal equilibrium at T = 0, (i.e. the gas particles are motionless.) Given enough time, the electromagnetic repulsion between the dust particles, combined with the containment potential, will cause the particles to gradually fall into a stable or metastable ground state, which is then analyzed quantitatively.
The parameter values used in this study are the same as those given by Qiao and Hyde (2005) in their development of an 11-particle phase diagram. The process used to develop a 12-particle phase diagram was to conduct multiple runs at varying Debye lengths with a fixed particle charge q = 3.84 × 10-16 C and fixed confinement parameter k = 2000 kg/C∙s2. For each Debye length examined, fifty clusters were created using box_tree and then analyzed.
The data from box_tree was output in the form of a table containing the position of each dust particle, as well as the net charge on each. This data was used to calculate the potential energy of the system, which is dependent on the charge on each particle and the distance between each particle. After calculating the potential energy for each cluster, the clusters were separated into one of two groups: one-shelled structures or two-shelled structures. The average potential for all single-shell structures was then compared to the average for all double-shell structures, so that a transition point could be determined. Based on this transition value, a more precise transition value was found by focusing on a narrow range of Debye lengths around the initial transition result.
III. RESULTS
Figure II. Difference in potential energy between one-shell and two-shell states of 12-particle system at various Debye lengths
Figure II shows the difference in energy between the twoone-shell state and the onetwo-shell state. As can be seen in the figure, the values are positive for λD < 225 μmλD < 225 μm, implying that the two-shell structure can be considered the ground state, with the one-shell structure a metastable state. For λD > 225 μmλD > 225 μm, the values are negative, so the one-shell structure is now the ground state, and the two-shell is a metastable state. Therefore, under these conditions, a 12-particle cluster will transition from one shell to two shells at λD ≈ 225μmλD ≈ 225 μm. A summary of the energy of both states at each Debye length can be found in Table I.
Table I. Potential energy for the one and two-shell states of a 12-particle system calculated for various Debye lengths.
IV. CONCLUSIONS
In conclusion, the box_tree code was used to form three-dimensional Yukawa crystals in a parabolic confinement potential. With a constant confinement parameter of k = 2000 kg/C∙s2 and a constant particle charge of q = 3.84 × 10-16 C, systems of 12-particles were simulated at varying Debye lengths. Previous studies [Qiao & Hyde 2005](Qiao & Hyde 2005) have shown the dependence of cluster structure on Debye length, but this study is the first to quantify this dependence for a 12-particle system. Further studies will seek to quantify structural dependence on particle charge q and confinement strength k.
Qiao, K. and T.W. Hyde (2005) Structural phase transitions of three-dimensional shielded Coulomb Clusters (finite Yukawa system). Unpublished
Chu, J.H., and Lin I. (1994) Direct Observation of Coulomb Crystals and Liquids in Strongly Coupled rf Dusty Plasmas. Physical Review Letters 72, 25 4009-4012
Arp, O., D. Block, M. Bonitz, H. Fehske, V. Golubnychiy, S. Kosse, P. Ludwig, A. Melzer, and A. Piel, (2005) 3D Coulomb Balls: Experiment and Simulation. Journal of Physics: Conference Series 11, pp 234 - 247, 2005
Aurenhammer, F. (1991) Voronoi Diagrams a survey of a fundamental geometric data structure. ACM Computing Surveys 23, 3 345-405
Rafac, R., J. Schiffer, J. Hangst., D. Dubin, and D. Wales, (1991) Stable configurations of confined cold ionic systems. Proceedings of the National Academy of Science 88 pp 483 486